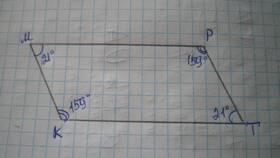
В параллелограмме углы обладают определенными свойствами, которые позволяют вычислять их суммы без дополнительных измерений. Рассмотрим основные закономерности.
Содержание
Основные свойства углов параллелограмма
- Противоположные углы равны
- Сумма соседних углов составляет 180°
- Сумма всех внутренних углов равна 360°
Варианты сумм двух углов
| Тип углов | Сумма | Обоснование |
| Два противоположных угла | 2α | α + α = 2α (по свойству равенства противоположных углов) |
| Два соседних угла | 180° | α + (180° - α) = 180° (как односторонние при параллельных прямых) |
| Любые два угла | 180° или 2α | Зависит от выбора углов (соседние или противоположные) |
Пример расчета
Дан параллелограмм ABCD с углом A = 65°. Найти суммы пар углов:
- ∠A + ∠C = 65° + 65° = 130° (противоположные углы)
- ∠A + ∠B = 65° + 115° = 180° (соседние углы)
- ∠B + ∠D = 115° + 115° = 230° (противоположные углы)
Геометрическое доказательство
Свойства углов параллелограмма вытекают из его определения:
- Параллелограмм - четырехугольник с попарно параллельными сторонами
- Параллельные стороны образуют односторонние углы
- Сумма односторонних углов при параллельных прямых равна 180°
Практическое применение
Знание этих свойств позволяет:
- Находить неизвестные углы параллелограмма
- Решать задачи на построение
- Доказывать равенство треугольников
- Решать задачи на вычисление площадей